Kapitel 12 Logistisk regression
När den oberoende variabel är numerisk och den beroende variabel dikotom och således enbart kan anta två värden har man traditionellt använt sig av analysmetoden logistisk regression. Här nedan följer först instruktioner hur man utför en enkel logistisk regression och som sedan följs upp av instruktioner hur man genomför en multipel logistisk regression.
12.1 Enkel logistisk regression
I detta exempel kommer att använda oss av Pathways to desistance-datasetet. Den frågeställning vi ställer är följande: Finns det ett samband mellan att ha skjutit en annan person och att ha en pappa som lagförts för ett brott?” Ett annat sätt att formulera frågan är: Kan vi predicera huruvida en individ har skjutit en annan person utifrån information om faderns lagföringshistorik?
Den beroende variabeln är dikotom och kan anta värdet 0 om individen ej har skjutit en annan person och 1 om personen tidigare har skjutit en annan person. Den oberoende variabeln antar värdet 0 om personens fader aldrig tidigare lagförts för ett brott och 1 om fadern har tidigare lagförts för ett brott. För att genomföra den enkla logistiska regressionen gör ni som följande:
Analyze > Regression > Binary Logistic
Därefter placerar ni den beroende variabeln - skjutit en annan person - i Dependent-fältet och den oberoende variabeln - lagförd fader - i Covariates-fältet.
Inte helt oväntat kommer ni få ut en rad olika rutor med en mängd information. Vi tar en i taget. Rutan Case Processing Summary ger er deskriptiv information om hur många individer som förekommer i analysen samt hur många som är missing. I rutan Dependent Variable Coding framgår det hur SPSS har valt att koda om den beroende variabeln så att den verkligen enbart antar värdena 0 och 1. Därefter kommer rad rutor under Block 0: Beginning Block. Block 0 är den logistiska modellen utan en oberoende variabel. Det vill säga en modell med enbart interceptet (och dess information om individen skjutit någon eller ej). Vi kan hoppa över hela Block 0 eftersom ingen information där är av intresse för oss.
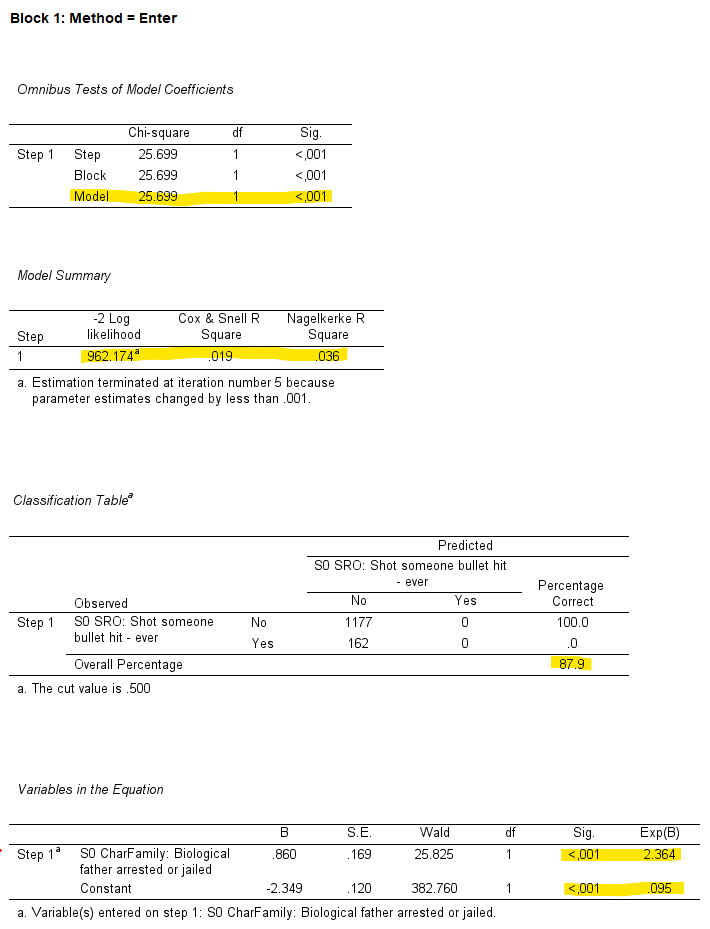
Under Block 1: Method = Enter börjar det bli lite intressantare. Under Omnibus Tests of Model Coefficients och det tillhörande P-värdet för Model hittar ni information om vår angivna modell presterar bättre än en modell utan vår oberoende variabel. Det motsvarar informationen i ANOVA-rutang ällande f-färdet och p-värdet för regressionsmodellen när ni utför en regressionsanalys (se kapitlet om enkel och multipel regression). Vi kan i vårt fall se att vår modell är signifikant. Under Model Summary hittar ni information om hur pass bra er logistiska modell passar er data. Cox & Snell R Square och Nagelkerke R Square är så kallade pseudo-R2 som ska efterlikna R2-värdet man får ut när man genomför en regressionanalys. Värdena för pseudo-R2 kan dock inte tolkas som estimat för förklarad varians. Enklast är istället att tänka att värdena kan gå från 0 till 1 och att höga värden indikerar att de oberoende variablerna är bättre på att predicera den beroende variabeln. I vårt fall har vi överlag ganska låga värden vilket betyder att även om den kan hjälpa oss predicera den beroende variabel så är dess prediktiva förmåga låg. -2 Log Likelihood är lite svårare att tolka men enkelt uttryck kan man säga att ju lägre värde desto bättre.
Under Classification Table hittar ni information om hur ofta (uttryckt i procent) som vår modell lyckades predicera rätt att en individ skjutit en annan person (alternativt ej) utifrån information om faders tidigare lagföring. Vår modell lyckades pricka rätt 87,9 % av fallen. Även om denna siffra är hög så ska det dock noteras att vår modell lyckades inte predicera att någon av våra individer som skjutit en annan person trots att vi faktiskt har 162 individer som gjort det. Det går att förklara med kombinationen att det är förhållandevis få som skjutit en annan person och det faktu att vi har en oberoende variabel som har en låg prediktiv förmåga.
Nu kommer vi äntligen till den viktigaste rutan: Variables in the Equation. Här ser vi information gällande vår hypotesprövning så som vilken effekt vår oberoende variabel har på vår beroende samt om denna effekt är statistisk signifikant. När vi utför en logistisk regression uttrycks betakoefficienten i termer av så kallade logaritmerade odds . Att tolka logaritmerade värden är minst sagt krångligt så därför brukar man ta exponenten av de logaritmerade värdena så att man får ut oddskvoter vilka är icke-logaritmerad. Dessa värden hittar ni under Exp(B). Enklaste sättet att tolka dessa koeffeicitenter är att värden som överstiger 1 visar positiva samband och värden som understiger 1 visar negativa samband. Ett värd på 1 visar inget samband alls. Eftersom vår oberoende variabeln har koefficienten 2.364 så har vi ett positivt förhållande: det finns ett samband mellan att ha en lagförd fader och att ha skjutit en annan person. Eftersom p-värdet är < .001 är detta samband statistiskt signifikant.
Överkurs: En nackdel med logistisk regression är att koefficienterna man får ut kan te sig svårtolkade. Som beskrivet här ovan finns två sätt att beskriva koefficienter från en logistisk regression. Vad som avgör vilken av de två sätten är om man använder sig av de logaritmerade oddsen (B i SPSS-outputen) eller om man väljer att titta på de koefficienten som - genom att ta exponenten av koefficienten - transformerats till oddskvoter. Denna transformering gör SPSS åt en och finns under Exp(B)).
Vi börjar med tolkningen av koefficienter som är logaritmerade. I vårt exempel är koefficienten .86. Vad den säger är att när vår oberoende variabel ökar med en enhet (vilket i vårt fall innebär de vars fader är lagförd) så ökar logaritmen av oddset att skjuta en annan person med .86. Ett annat sätt att uttrycka det är att logaritmen av oddset att skjuta en annan person ökar med 86 procent (.86*100). Notera att vi ej talar om procentenheter utan procent.
Även om ovanstående beskrivning begripliggör koefficienten en aning så kan det fortfarande vara svårt att förstå förändringar av logaritmerade odds vilket är anledningen till varför man istället ta exponenten av koefficienten (se Exp(b)) vilket då uttrycker oddskvoter.
Oddskvoter innebär kortfattat oddsförhållandet mellan två grupper. Föreställ att du har två grupper: Grupp 1 vars fader ej är lagförd och grupp 2 vars fader är lagförd. I grupp 1 är sannolikheten att en sak ska hända ,5 (och därför sannolikheten att denna sak ej ska hända ,5). Oddset är då 1 (,5 / ,5). I grupp 2 är sannolikheten ,67 att samma sak ska hända. Oddset är då 2 (,67/,33). Om vi delar grupp 2:s odds med grupp 1:s odds får vi 2 / 1 = 2. Detta är oddskvoten mellan dessa två grupper. Det vill säga ett dubbelt så högt odds att saken i fråga ska hända för grupp 1 jämfört med grupp 2.
I vårt exempel är exponenten av koefficienten - Exp(b) - 2.364. Det betyder att oddset att skjuta någon är 2.364 gånger högre för någon som har en lagförd fader jämfört med någon som ej har en lagförd fader. Alternativt om man önskar att uttrycka det i procent kan man säga att oddset att skjuta någon är 136,4 procent högre ((2.364-1)* 100) för någon som har en lagförd fader jämfört med någon som ej har en lagförd fader.
Av pedagogiska skäl har vi som sagt valt en dikotom oberoende variabel men hur skulle man tolka koefficienten om den var kontinuerlig istället? Säg att den oberoende variabeln är antal lagförda vänner och att koefficienten fortfarande är 2.364. Koefficienten beskriver då hur mycket oddskvoten ökar för varje enhets ökning av den oberoende variabeln. En individ med 10 lagförda vänner har då 23.64 gånger högre odds (2.364x10) att ha skjutit någon än en individ med inga lagförda vänner.
12.2 Multipel logistisk regression
Nu är det dags att inkludera en ytterligare variabel till vår modell. Kan det kanske teoretiskt vara så att det finns en viss könsskillnad i den effekt som faderns lagföring har på risken att ha skjutit någon annan? Det kanske är så att pojkar löper högre risk eftersom det teoretiskt kan vara så att pojkar tar efter sin fader i högre utsträckning än flickor gör. För att justera/kontrollera för denna effekt inkluderar vi därför variabeln kön i vår modell.
Innan vi utför vår logistiska regression behöver vi koda om könsvariabel. I nulägt är 1 = male och 2 = female. Vi gör om den så att 0 = female och 1 = male (se kapitlet databearbetning).
Vi gör i princip på samma sätt som tidigare:
Analyze > Regression > Binary Logistic
Vi börjar med att placerar vår beroende varibel - skjutit annan person - i Dependent-fältet. För att kunna se hur vår koefficient för lagförd fader förändras när vi går från en enkel till multipel logistisk regression så väljer vi att ha två modeller. Börja med att placera enbart den oberoende variabeln lagförd fader i Block 1-rutan. Tryck sedan på next och lägg på nytt den oberoende variabeln lagförd fader i rutan som nu dock heter Block 2. Placera därefter även in den obeoende variabeln kön i samma ruta. Tryck därefter på OK.
Precis som tidigare så får vi en uppsjö av rutor och denna gången även fler. Vi hoppar direkt ner till Block 1: Method = Enter (eftersom de föregående rutorna har vi samtliga redan gått igenom). Denna ruta är vår enkla logistiska regression och är således identisk med den som vi utförde här ovan. Alla värden ska vara identiska som i den enkla logistiska regressionen. Eftersom inget har förändrats här så går vi raskt över till Block 2: Method = Enter vilket är vår multipla logistiska regressions som innehåller modellen med våra två oberoende variabler.
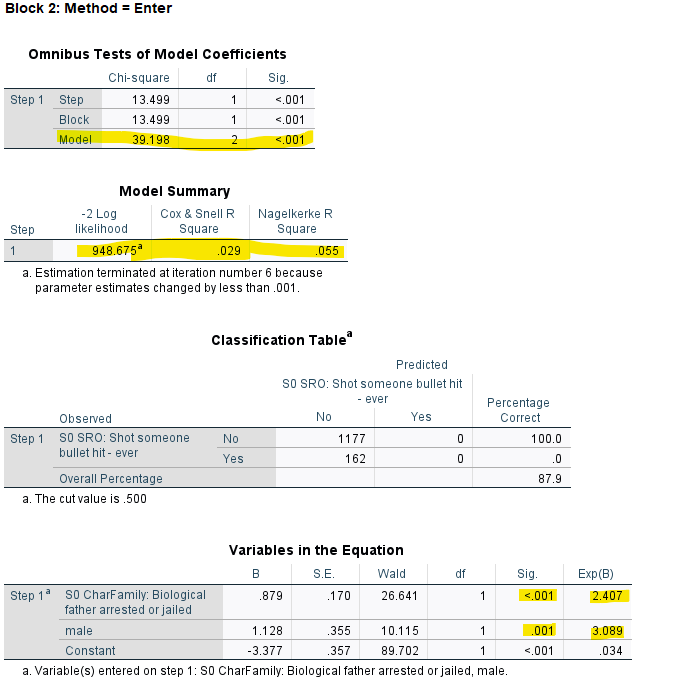
Det vi kan se se är att den effekt som en faders lagföring har på ens sannolikhet att ha skjutit en annan person inte förändras nämnvärt när vi konstanthåller för kön. Effekten är fortfarande fortfarande signifikant.